In my previous post I made mention about a new character type nicknamed “Brute.” Since then that character has become known as Omega. The special trait the Omega has is these thick ripples that bursts out when omega slams down. They don’t have that much range but they last for a few seconds. Since Omega’s ripples are thicker, there is more surface area that can damage the opponent. So that means thickness needs to be taken into account.
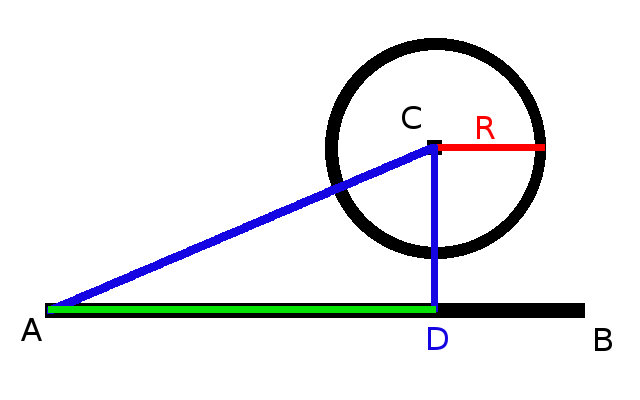
Going back to the last post on collision, we had three checks that needed to pass if a collision was to be successful.
Check One: ||DA|| <= ||BA||
Check Two: If DA and BA are in the same direction.
Check Three: ||DC|| <= R
These checks give us a simple solution for solving this collision, but it neglects some things.
Checks one and two don’t take into do not take into account when D is slightly passed B or slightly before A, such that there would still be a collision if the radius was close enough. But this can easily be taken into account with a distance check from the center of the circle to the point.
The third check neglects the thickness of the line. This will need to be fixed if Omega’s ability is to work properly. Luckily, that can be fixed easy enough in itself by adding the thickness to the equation. So, ||DC|| <= R just becomes ||DC|| <= R + T where T is the thickness of the line.
With these modifications to the collision checking, the formula will now be able to handle the special ripples that Omega creates.